Asymptotic space-time symmetries in 2+1 and 3+1 dimensions
In the 1960s, Bondi, van der Burg, Metzner, and Sachs (hence the acronym BMS) made an astonishing discovery that asomptotically – i.e. at infinity – space-time may possess an infinitelly richer symmetry structure than the known from the relativity theory and gravity theory Poincare group. However, the meaning and consequences of this result have only begun to be fully realised in the past two decades, including in the broader context of generalisation of the BMS symmetry group showcased by Barnich and Troessaert in that time. Similarly, this recent period has brought a significant increase in interest in work on the description of space-time and theories defined on it (in particular, gravity theory) in Galileo’s and Carroll’s approximations, formalised as early as the 1960s. The former approximation is used in case when velocities in the system are negligibly low in comparison to the speed of light c, which corresponds to Newtonian physics; the latter – when velocities are close to c, which leads to the so-called ultralocal physics.
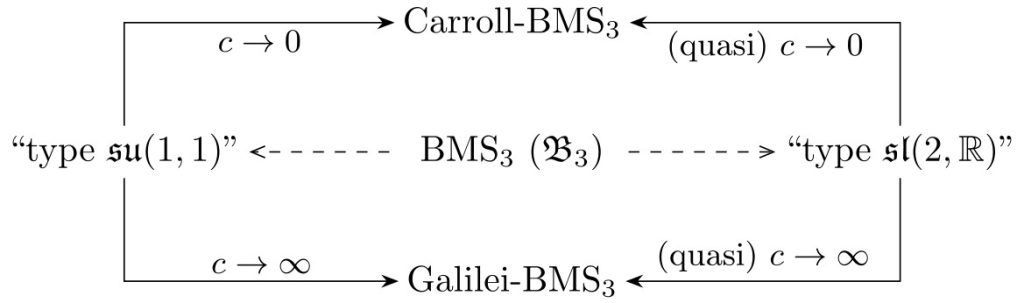
The results included in the article “On Carrollian and Galilean contractions of BMS algebra in 3 and 4 dimensions” by Andrzej Borowiec, Jerzy Kowalski-Glikman, and Tomasz Trześniewski, published in Classical and Quantum Gravity lie at the intersection of the two research areas outlined above. Namely, they concern the construction of Galilean and Carrollian contractions of symmetry algebras: BMS in 2+1 dimensions, Lambda-BMS in 2+1 dimensions (generalisation of BMS with non-zero cosmological constant), and BMS in 3+1 dimensions. It was shown that in the first case both kinds of contractions exist (so it is possible to obtain Carroll-BMS and Galileo-BMS algebras), only Galilean in the second, and in the third it is limited to the possibility of defining quasi-Carrollian and quasi-Galilean contractions.
Research funded by the National Science Centre, project no. UMO-2022/45/B/ST2/01067 (A.B. and T.T.) and project no. 2019/33/B/ST2/00050 (J.K.G.).
