Classification of non-Lorentzian quantum symmetries in 2+1 dimensions

Space-time symmetries constitute a key component of fundamental physical theories, such as classic and quantum electrodynamics, or the general relativity theory (classic gravitational field theory). The most basic of them are described by the Lorentz group (for a non-zero cosmological constant, it generalizes to the de Sitter or anti-de Sitter group), keeping the value of the speed of light c. On the other hand, if we consider the so-called Galilei limit, where c tends to infinity, we reduce the given theory to classic Newtonian physics where time is absolute. The opposite option is taking the limit of c going to zero, known as the Carroll limit, which leads to ultralocal physics without a causal link between different points in space. Those two extreme cases that can be collectively called non-lorentzian recently became the object of active interest of theorists because they turn out to play an essential role in many advanced issues.

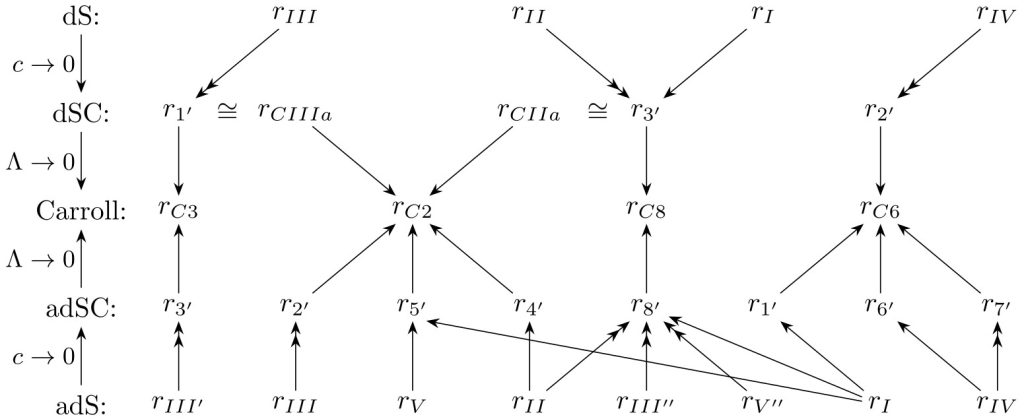
Meanwhile, in the context of seeking the quantum gravity theory spacetime symmetry deformations are being introduced, which is enabled to us by the formalism of quantum groups. The paper Quantum symmetries in 2+1 dimensions: Carroll, (a)dS-Carroll, Galilei and (a)dS-Galilei by Tomasz Trześniewski, published in the Journal of High Energy Physics, generalises the Galilei and Carroll limits (using the quantum contractions procedure and adequate isomorphisms) into all the quantum symmetries identifiable for the 2+1-dimensional space-time with a zero, positive, or negative cosmological constant. The case of three dimensions is not just a test arena for working in four, but it is also interesting in its own right due to the gravity theory reduced to it, in which quantum symmetries already emerge on the classic level.