Study of the convergence of the Meshless Lattice Boltzmann Method
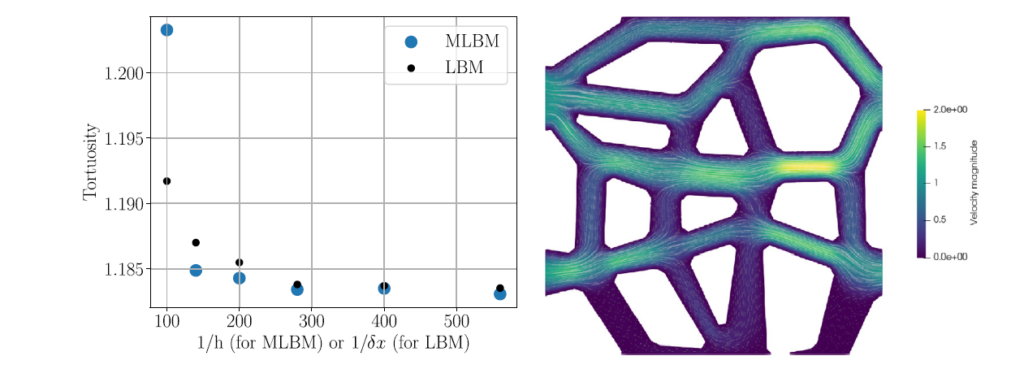
Graph: Convergence of the hydrodynamic curvature in the duct system with the system size for the duct system on the right side (velocity field in the pore space) calculated with the meshless LBM solver.
Complex geological processes, forecasting weather, modeling of the blood flow in the cardiovascular system or medicine in the cerebral cortex – the greatest problems of modern civilization are in some way connected with transportation of fluids. One of the basic tools for analyzing hydrodynamic systems in terms of fluid transport are numerical methods. Standard grid methods, where differential equations are solved on regular or irregular grids, often fail – the grids are very large, their generation requires massive processing power, memory, and not infrequently manual repair of faulty elements.
In our recent work we performed convergence studies of the meshless Boltzmann gas method – a relatively young numeric method that made it possible to formulate a solution without the need to generate a computational grid. Within this work we discussed how the accuracy of the result increases with the size of the system and how its properties present themselves in comparison to the standard approach.
Using this method we have solved two physical problems – flow in a circular channel and flow and calculation of hydrodynamic curvature in a network of connected channels.
The work was done under the grant NCN Opus LAP 2021/43/I/ST3/00228
