Studies on dark matter

In the article titled Polarized target as a tool for probing the non-standard properties of dark matter published in the journal Physics of the Dark Universe Volume 41, August 2023, 101242, Arkadiusz Błaut and Wiesław Sobków study the properties of dark matter.

In the work we examine the possibility of applying a polarised nuclear shield in testing non-standard properties of fermionic dark matter. We assume that vector, axial, scalar, and tensor interactions take part in the process of dark matter scattering. We analyse energy and angle distributions of recoil nuclei for four experimental configurations determined by assumptions for measuring dark matter polarization and nuclear spin. In the first case, we assume that dark matter is unpolarized, and the spin of the scattered nucleus is not measured. The second option assumes measurement of its spin. The third variant permits hypothetical polarisation of dark matter; in this case the measurement is insensitive to nucleus polarisation. In the fourth experiment we assume the presence of polarised dark matter and possibility of measurement of nucleus spin. Each of the listed measurement scenarios offers new ways of testing dark matter properties and its interactions with visible matter molecules. In particular, measurements of angular distributions can be used to detect symmetry violations against time reversals.

Figure 1: Kinematics of polarized DM-nucleus scattering. vˆ_e is the Earth’s velocity in the galactic rest frame; sˆ₁ is the polarization vector of the nuclear target; v^→_χ ,sˆ₂ – velocity and polarization vector of the DM incoming from the direction defined by the angles θ, ϕ; v^→, sˆ₃ – velocity and polarization of the recoil nucleus outgoing in the direction defined by the angles α, β.

;

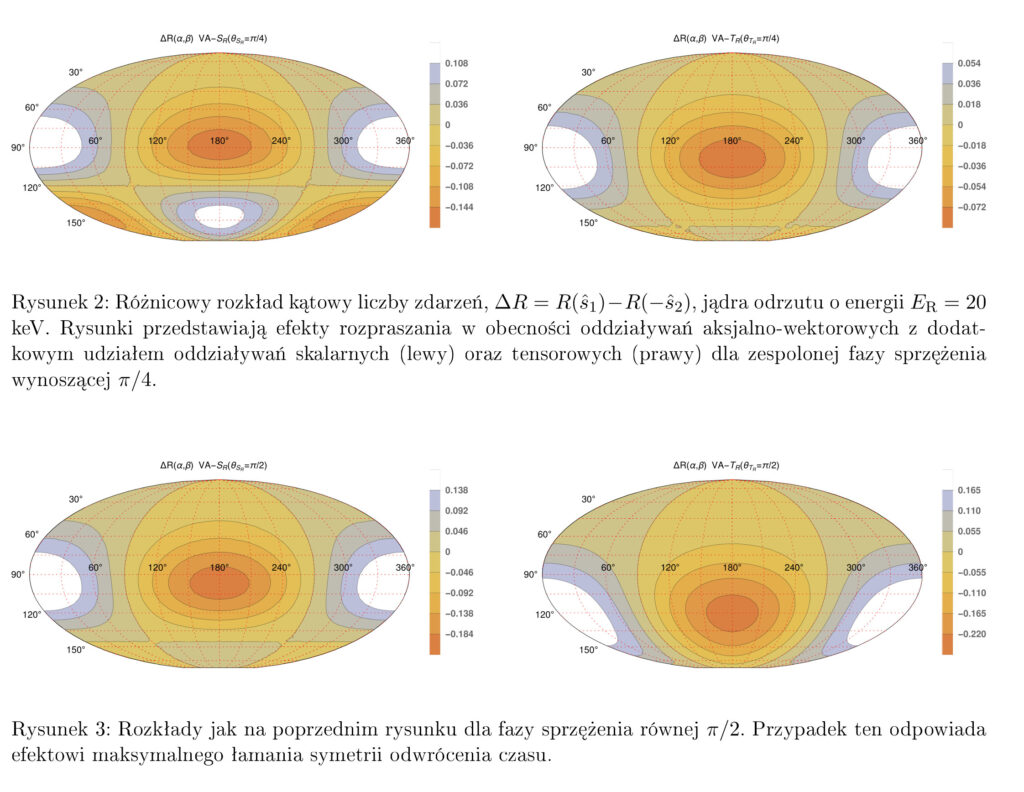
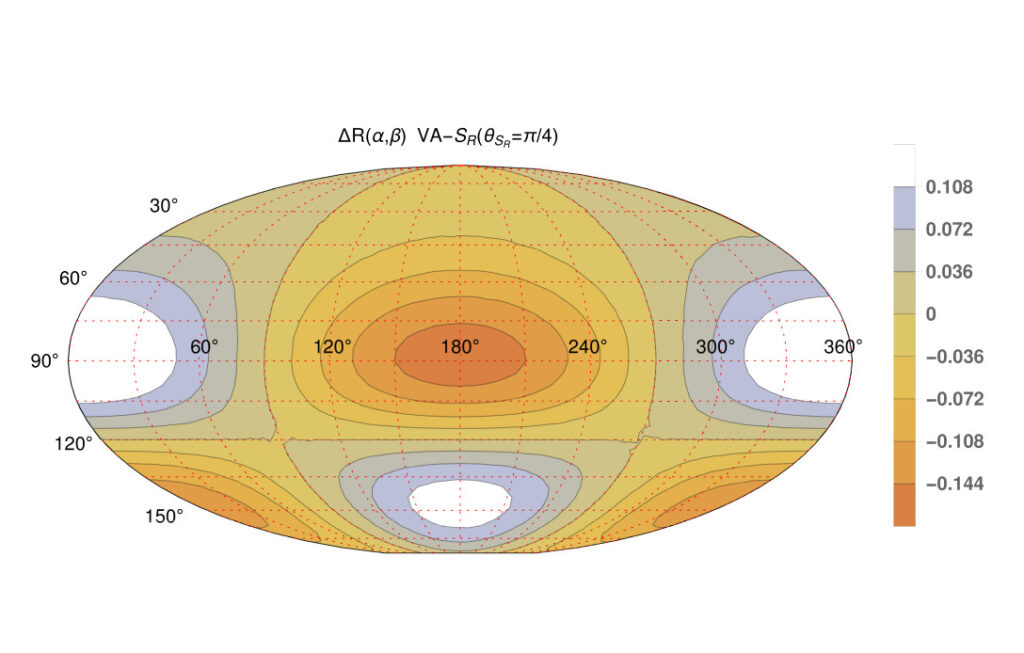
Figure 2: Differential angular distribution of the number of events, ΔR = R(s^{^}₁) – R(-s^{^}₂), recoil nuclei with energy E_R = 20 keV. The graphs present the effects of scattering in the presence of axial-vector interactions with an additional involvement of scalar (left) and tensor (right) interactions for combined coupling phase of 𝝅/4.

Figure 3: Distributions as in the previous figure for combined coupling phase of 𝝅/2. This case corresponds to the effect of maximum symmetry breaking time reversal.