The vast majority of massive stars (i.e. those whose initial mass exceeds around eight masses of the Sun and that explode as supernovas in the future) do not occur in the Universe alone but in binary or even multiple systems.

For this reason the evolution of massive stars is intrinsic to  their duality that leads to an array of interesting interactions between components, among others to mass exchange, shared envelope phase, or even two stars merging into one.

However, it is very complicated to predict the evolution of massive binary systems because it is necessary to consider many interconnected phenomena.

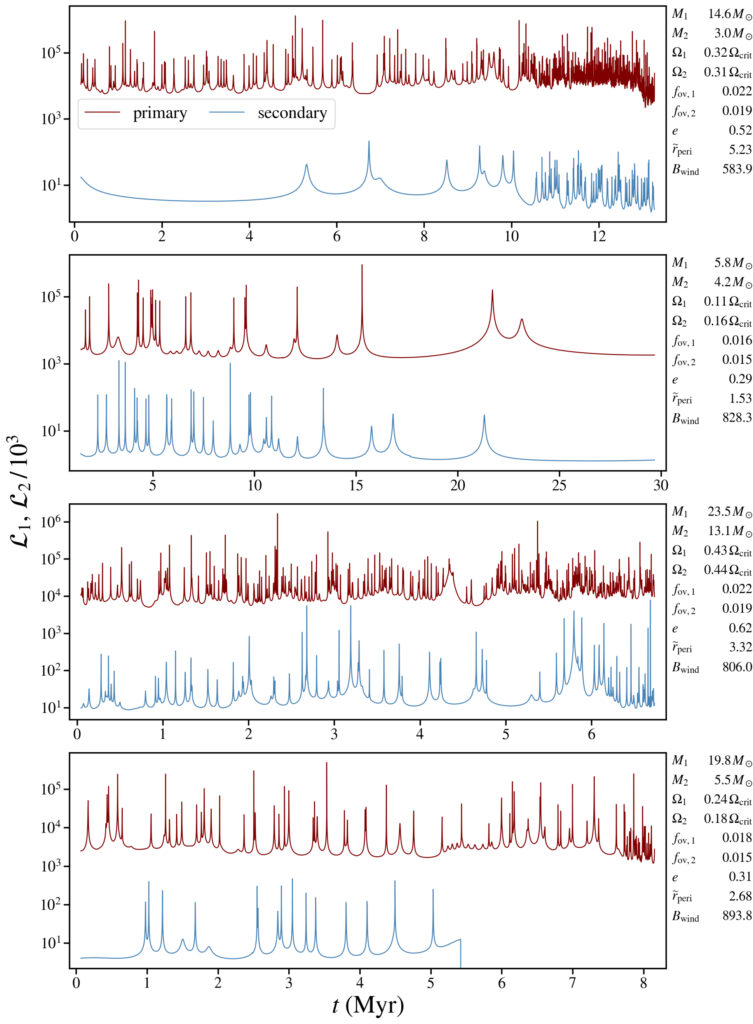
In our work we analyze the phenomenon of resonances between tidal forces in massive eccentric binary systems and the spectrum of oscillations of its own components.

When one of the pulsation frequencies of the star enters resonance with the orbital frequency of the system, we observe so-called tidally excited oscillations, which can contribute to accelerated tightening and circularization of the orbit. This is the first time we have performed this type of analysis based on simulations of the evolution of many tens of thousands of massive binary systems.

Through our simulations, we have learned that it is the most massive of the stars we have analyzed that should most often “fall” into this type of resonance. Moreover, tidally excited oscillations should be common and particularly relevant to the evolution of massive binary systems when one of its components has already practically burned all of its hydrogen “fuel” in the nucleus.

The publication by P. A. Kołaczek-Szymański and T. Różański is available to read at: