Study of the knot-quiver correspondence

In the paper titled Permutohedra for knots and quivers published by Jakub Jankowski, Piotr Kucharski, Helder Larraguível, Dmitry Noshchenko, and Piotr Sułkowski in the journal Phys. Rev. D 104, 086017 (2021) the authors study the knot-quiver correspondence.

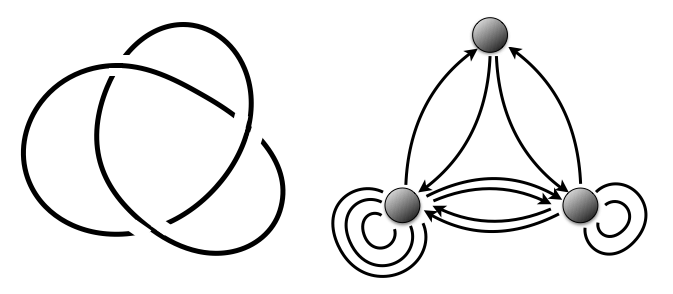
Rys. 1 Węzeł trój-listnik (z lewej), posiadający trzy przecięcia. Z prawej odpowiadający mu kołczan złożony z trzech wierzchołków oraz zestawu krawędzi i pętli. — Fig. 1 Trefoil knot (left) with three intersections. On the right a corresponding quiver, consisting of three peaks and a set of edges and loops.

Knots are closed loops placed in three-dimensional space, characterised by the number of intersections. For instance, the knot in Fig. 1 has three intersections and is the simplest non-trivial knot, and the only one with three intersections. Due to its shape it is called a trefoil.The fundamental and unresolved issue of knot theory is their classification and distinction that mathematicians carry out by assigning to knots various objects called topological invariants. Over decades a multitude of various kinds of invariants of larger or lesser use appeared, but the ideal one that would help to distinguish any two knots remains elusive.

The knowledge obtained in this way is available in the catalogue of knots on the website

A huge surprise was the discovery of correspondence between certain physical values and knot invariants in the late 1980s by Edward Witten. Inspirations from physics have been an important branch in development of knot theory ever since, generating significant progress in mathematics. Part of this progress was characterising a whole array of invariants with the so-called quivers. Quivers in mathematics are something else than what Robin Hood used; they are graphs composed of a finite number of peaks connected with a defined number of arrows. It turns out that such objects are incredibly useful in defining knot theory invariants and that each knot seems to have a corresponding quiver. For instance, the simplest knot in Fig. 1 is assigned to a quiver composed of three peaks and a set of lines (the convergence of the number of the intersections of the knot and the peaks is coincidental).

Rys. 2 Równoważne kołczany dla węzła o dziewięciu przecięciach. Każda niebieska kropka oznacza jeden kołczan, a kolorowe połączenia operacje symetrii między kołczanami. — Fig. 2 Equivalent quivers for a knot with nine intersections. Each blue dot denotes one quiver while the colourful lines mark operations of symmetries between the quivers.

In the described paper the task was to study whether the knot-quiver correspondence is unambiguous, i.e. whether each knot has exactly one assigned quiver, and if not then is there an equivalent quiver structure? To our surprise it turned out that not only the correspondence of knots and quivers is not unambiguous, but also that a very large number of equivalent quivers may correspond to a single knot! For instance, for knots with six intersections this number reaches 100 000! Moreover, it turns out that equivalent quivers display a beautiful geometrical structure that is a multi-dimensional generalisation of a regular polyhedron, an example of which is in Fig. 2, presenting equivalent quivers for a knot with nine intersections. The meaning of those structures and their consequences for the physical as well as mathematical aspects of the issue are the topic of current studies.

Added by: Joanna Molenda-Żakowicz

Dean’s representative for promotion and media relations