
Badanie relacji węzeł – kołczan
W pracy pt. „Permutohedra for knots and quivers” opublikowanej przez Jakuba Jankowskiego, Piotr Kucharskiego, Helder Larragu vel , Dmitry Noshchenko i Piotra Sułkowskiego w czasopiśmie Phys. Rev. D 104, 086017 (2021) autorzy badają relację węzeł-kołczan.
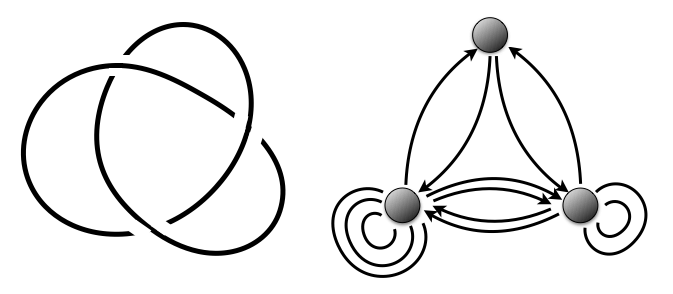
Węzły to zamknięte pętle umieszczone w trójwymiarowej przestrzeni, scharakteryzowane liczbą przecięć. Dla przykładu węzeł z Rys. 1 ma trzy przecięcia i jest najprostszym nietrywialnym węzłem i jedynym o trzech przecięciach. Z uwagi na swój kształt nosi nazwę trój-listnika (ang. trefoil, czyli koniczyna). Podstawowym i nierozwiązanym zagadnieniem teorii węzłów jest ich klasyfikacja i rozróżnienie, których matematycy dokonują poprzez przypisanie węzłom rozmaitych obiektów zwanych niezmiennikami topologicznymi. Przez dekady pojawiła się cała mnogość różnego rodzaju niezmienników o większym lub mniejszym zastosowaniu, jednak ten idealny, za pomocą którego będzie można rozróżnić dowolne dwa węzły jest wciąż nieuchwytny.
Ogromnym zaskoczeniem okazało się odkrycie związku między pewnymi wielkościami fizycznymi a niezmiennikami węzłów zapoczątkowane pod koniec lat osiemdziesiątych przez Edwarda Wittena. Od tamtego czasu inspiracje fizyką stanowiły ważną gałąź rozwoju teorii węzłów generując istotny postęp w matematyce. Częścią tego postępu było scharakteryzowanie całego szeregu niezmienników za pomocą tzw. kołczanów (ang. quiver). Kołczany, to w matematyce coś innego niż używał Robin Hood; to grafy złożone ze skończonej liczby wierzchołków połączonych określoną liczbą strzałek. Okazuje się, że takie obiekty są niezwykle użyteczne do opisu niezmienników teorii węzłów i że każdy węzeł zdaje się mieć odpowiadający mu kołczan. Dla przykładu najprostszy węzeł z Rys. 1 jest przyporządkowany kołczanowi złożonemu z trzech wierzchołków i zestawu linii (zbieżność liczby przecięć węzła i wierzchołków jest przypadkowa).
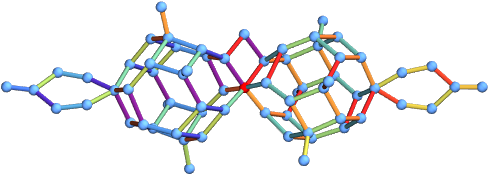
metrii między kołczanami.
W opisywanej pracy zdaniem było zbadanie, czy relacja węzeł-kołczan jest jednoznaczna, tzn. czy każdy węzeł ma przyporządkowany dokładnie jeden kołczan, a jeśli nie to czy jest jakaś struktura równoważnych kołczanów? Ku naszemu zdumieniu okazało się, że nie tylko relacja węzłów i kołczanów nie jest jednoznaczna, ale że pojedynczemu węzłowi może odpowiadać bardzo duża liczba równoważnych kołczanów! Dla przykładu dla węzłów o sześciu przecięciach ta liczba sięga 100 000! Co więcej, okazuje się że równoważne kołczany wykazują piękną strukturę geometryczną będącą wielowymiarowym uogólnieniem wielościanu foremnego, przykład którego znajduje się na Rys. 2, który przedstawia równoważne kołczany dla węzła o dziewięciu przecięciach. Znaczenie tych struktur i ich konsekwencje dla fizycznych jak i matematycznych aspektów zagadnienia stanowią temat bieżących badań.
Dodała: Joanna Molenda-Żakowicz
Pełnomocnik Dziekana ds. promocji i kontaktów z mediami
