Asymptotyczne symetrie czasoprzestrzeni w 2+1 i 3+1 wymiarach
W latach 60-tych, Bondi, van der Burg, Metzner i Sachs (stąd akronim BMS) dokonali zaskakującego odkrycia, że asymptotycznie – czyli w nieskończoności – czasoprzestrzeń może posiadać nieskończenie bogatszą strukturę symetrii, niż znana z teorii względności oraz teorii grawitacji grupa Poincare. Jednakże, znaczenie i konsekwencje tego rezultatu zaczęto sobie pełniej uświadamiać dopiero od dwóch dekad, również w szerszym kontekście uogólnienia grupy symetrii BMS, które w tym czasie pokazali Barnich i Troessaert. Podobnie, to ostatni okres przyniósł znaczny wzrost zainteresowania pracami nad opisem czasoprzestrzeni i zdefiniowanych na niej teorii (w szczególności, teorii grawitacji) w przybliżeniach Galileusza oraz Carrolla, sformalizowanych już w latach 60-tych. Pierwsze wspomniane przybliżenie stosuje się w przypadku, gdy prędkości w układzie są zaniedbywalnie małe w porównaniu do prędkości światła c, co odpowiada fizyce newtonowskiej; drugie – gdy prędkości są bliskie c, co prowadzi do tzw. fizyki ultralokalnej.
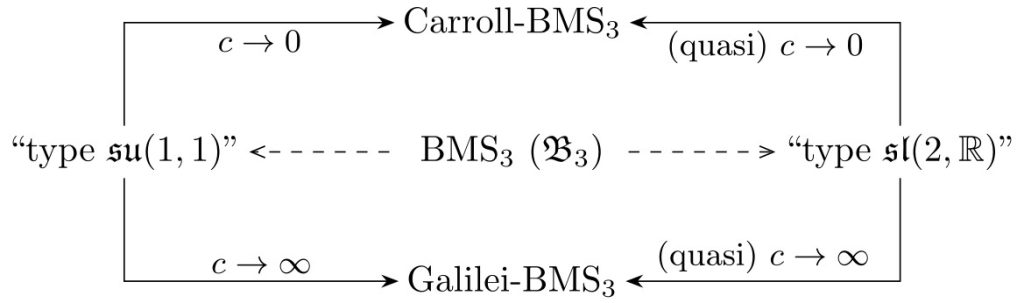
Wyniki zawarte w artykule „On Carrollian and Galilean contractions of BMS algebra in 3 and 4 dimensions” autorstwa Andrzeja Borowca, Jerzego Kowalskiego-Glikmana i Tomasza Trześniewskiego, opublikowanym w Classical and Quantum Gravity leżą na przecięciu wyżej przedstawionych dwóch obszarów badań. Mianowicie, dotyczą one konstrukcji Galileuszowskich i Carrollowskich kontrakcji algebr symetrii: BMS w 2+1 wymiarach, Lambda-BMS w 2+1 wymiarach (uogólnienie BMS przy niezerowej stałej kosmologicznej) i BMS w 3+1 wymiarach. Pokazano, że w pierwszym przypadku istnieją oba rodzaje kontrakcji (więc da się otrzymać algebry Carrolla-BMS i Galileusza-BMS), w drugim tylko Galileuszowska, a w trzecim ogranicza się to do możliwości zdefiniowania kontrakcji quasi-Carrollowskich i quasi-Galileuszowskich.
Badania finansowane przez Narodowe Centrum Nauki, projekt nr UMO-2022/45/B/ST2/01067 (A.B. i T.T.) oraz projekt nr 2019/33/B/ST2/00050 (J.K.G.).
