Klasyfikacja nie-lorentzowskich symetrii kwantowych w 2+1 wymiarach

Symetrie czasoprzestrzeni stanowią kluczowy składnik fundamentalnych teorii fizycznych, takich jak klasyczna i kwantowa elektrodynamika, czy ogólna teoria względności (klasyczna teoria pola grawitacyjnego). Najbardziej podstawowe z nich są opisywane przez grupę Poincare – inaczej niejednorodną grupę Lorentza (dla niezerowej stałej kosmologicznej uogólnia się ona do grupy de Sittera lub anty-de Sittera), zachowującą wartość prędkości światła c. Z drugiej strony, jeżeli rozważymy tzw. granicę Galileusza, w której c dąży do nieskończoności, redukujemy daną teorię do klasycznej fizyki Newtona, gdzie czas ma charakter absolutny. Przeciwną możliwością jest wzięcie granicy c dążącego do zera, znanej jako granica Carrolla, co prowadzi do fizyki ultralokalnej, bez związku przyczynowego pomiędzy różnymi punktami przestrzeni. Te dwa skrajne przypadki, które można wspólnie nazwać nie-lorentzowskimi stały się ostatnio przedmiotem aktywnego zainteresowania teoretyków, ponieważ okazują się odgrywać istotną rolę w wielu zaawansowanych zagadnieniach.

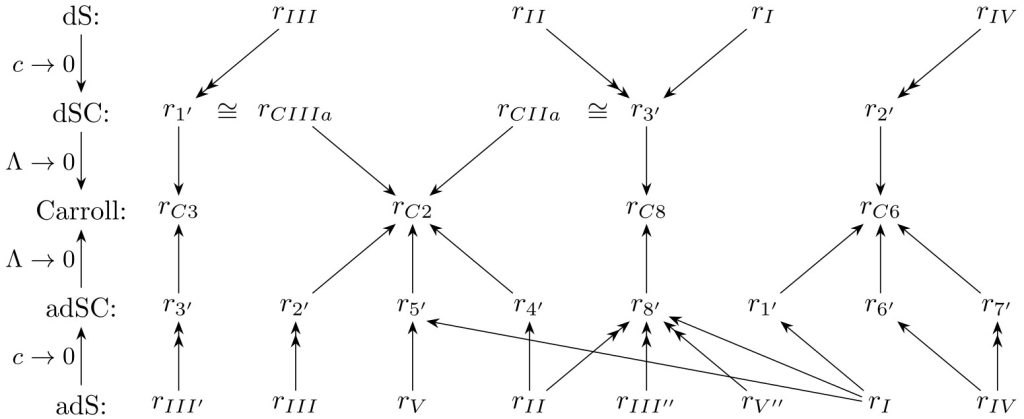
Tymczasem, w kontekście poszukiwań teorii grawitacji kwantowej wprowadza się deformacje symetrii czasoprzestrzeni, co umożliwia nam formalizm grup kwantowych. W artykule „Quantum symmetries in 2+1 dimensions: Carroll, (a)dS-Carroll, Galilei and (a)dS-Galilei” autorstwa Tomasza Trześniewskiego, opublikowanym w Journal of High Energy Physics dokonane zostało uogólnienie granic Galileusza i Carrolla (przy użyciu procedury kwantowych kontrakcji oraz odpowiednich izomorfizmów) na wszystkie symetrie kwantowe jakie da się zdefiniować dla 2+1-wymiarowej czasoprzestrzeni z zerową, dodatnią lub ujemną stałą kosmologiczną. Przypadek trzech wymiarów to nie tylko arena testowa dla pracy w czterech, ale jest on również interesujący sam w sobie, ze względu na własności zredukowanej do niego teorii grawitacji, w której symetrie kwantowe wyłaniają się już na poziomie klasycznym.

Badania finansowane przez Narodowe Centrum Nauki, projekt nr UMO-2022/45/B/ST2/01067.